3D моделирование напряженно-деформированного
состояния пневматических шин.
Группа 1. Б. Е. Победря, С. В. Шешенин, С. А. Маргарян,
Московский Государственный Университет, Россия
Механико-математический факультет, кафедра механики композитов.
Результаты,
полученных в ходу работы над проектом, докладывались на 8, 9, 10-м симпозиумах
"Проблемы шин резинокордных композитов", проходивших в НИИ шинной промышленности
(Москва, Россия, 1997, 98, 99).Доклады опубликованы в трудах симпозиумов.
В настоящем отчете описываются проведенная работа, полученные научные результаты
и разработанные программы. Основной практический результат состоит в том,
что разработана и реализована в виде программ методика расчета напряженно-
деформированного состояния шин в осесимметричной и трехмерной постановках.
Помимо этого финансовая поддержка ИНТАС позволила провести теоретико-практическое
исследование эффективности некоторых современных итерационных процессов
и начать исследования по их параллельной реализации.
Введение.
Трехмерное моделирование напряженно-деформированного состояния пневматических шин представляет интерес, по крайней мере, в двух аспектах. Во-первых, в чисто теоретическом, так как ставит интересные теоретические проблемы как в смысле механики композитов, так и в смысле вычислительной механики. По существу трехмерное моделирование шин является очень серьезным тестом для ряда численных алгоритмов. Особенно это касается итерационных методов. Во-вторых, эта задача интересна в практическом плане, так как в России распространен расчет шин на основе методов сопротивления материалов и, следовательно, выполнение проекта может внести вклад в становление современных расчетных методик на основе метода конечных элементов (МКЭ). В представляемом отчете развивается методика расчета напряженно-деформированного состояния резино-кордных пневматических шин на основе уравнений теории упругости, а не теории оболочек. Такое моделирование обладает явными достоинствами, так как не связано с гипотезами теории оболочек, пригодно для неоднородных, например, слоистых анизотропных тонкостенных тел. Точность численной реализации за счет увеличения числа узлов меньше зависит от толщины и внутренней структуры. Кроме этого, для численного решения уравнения упругости 2-ого порядка проще, чем уравнения теории оболочек. В связи со стремительным развитием компьютеров, их постоянным удешевлением такой подход приобретает все больший смысл. Стремительное повышение мощности персональных компьютеров, составляющих основной парк компьютеров в России, используемых для научных вычислений, дает новый импульс для реализации такого подхода. Целесообразность этого направления оправдывается также появлением многопроцессорных систем на основе платформы Win32, распространением на эту платформу программных средств распараллеливания вычислений на сети однопроцессорных PC .
С точки зрения механики шина представляет собой резинокордный композит, для моделирования которого следует применять математический аппарат механики композитов [12,13]. В настоящей работе для моделирования нагружения шины мы будем использовать уравнения нелинейной теории упругости. Для эффективной реализации трехмерного моделирования необходимо преодолеть, прежде всего, чисто теоретические проблемы. Дело в том, что резинокордный композит представляет собой очень сложную систему. Сложность состоит в том, что конструкция испытывает большие изменения геометрии, представляет собой неоднородную систему, резина обладает очень малой сжимаемостью. Для исследования были выбраны следующие задачи расчета НДС шины:
- Статическое нагружение внутренним давлением.
- Осадка шины под действием внутреннего давления и вертикальной силы.
- Учет сил трения при осадке.
Глава 1. Механическая модель для определения напряженно - деформированного состояния пневматических шин.
В этой главе рассматривается механическая модель напряженно - деформированного состояния (НДС) шины с использованием уравнения нелинейной теории упругости.
1. Постановка краевой задачи теории упругости при конечных деформациях.
Используем соотношение нелинейной
теории упругости [11] для описания поведения шины. Рассматривая шину как
неоднородное упругое тело, способное испытывать большие искажения геометрии,
будем использовать уравнения равновесия нелинейной теории упругости при
квазистатическом нагружении. В работе используется подход Лагранжа, т.
е. отображение текущей области ![]() ,
занимаемой телом в момент
,
занимаемой телом в момент ![]() ,
на начальную область
,
на начальную область ![]() .
Введем используемые в дальнейшем обозначения, следуя [11,14]. Пусть положение
материальной точки в начальном состоянии задается радиус вектором
.
Введем используемые в дальнейшем обозначения, следуя [11,14]. Пусть положение
материальной точки в начальном состоянии задается радиус вектором ![]()
![]() (1.1)
(1.1)
где ![]() -
лагранжевы координаты, а в момент
-
лагранжевы координаты, а в момент ![]() -
радиус вектором
-
радиус вектором ![]()
![]() (1.2)
(1.2)
![]()
Функции (1.1), (1.2) отображают
область ![]() (
(![]() при
при ![]() )
на некоторую область в пространстве переменных
)
на некоторую область в пространстве переменных ![]() .
В начальном и текущем состояниях определяются
.
В начальном и текущем состояниях определяются
локальный и взаимный базисы:
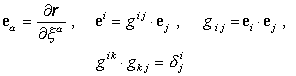 (1.3)
(1.3)
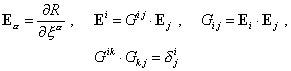 (1.4)
(1.4)
![]()
Операторы градиента в начальном и текущем состояниях определяются по формулам
![]() (1.5)
(1.5)
Тензор ![]() в
отечественной литературе называется градиентом места
в
отечественной литературе называется градиентом места
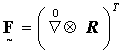
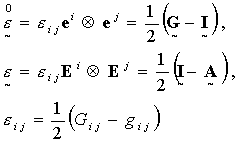 (1.6)
(1.6)момент времени и имеющей известную границу. При этом отображении возникает тензор напряжений Пиолы
плотность в деформированном состоянии, ![]() -
массовые силы, которыми при моделировании НДС шины могут являться силы
инерции,
-
массовые силы, которыми при моделировании НДС шины могут являться силы
инерции, ![]() -
якобиан преобразования геометрии от начальной конфигурации к текущей.
-
якобиан преобразования геометрии от начальной конфигурации к текущей.
![]()
При моделировании активного квазистатического деформирования будем использовать потенциальную форму определяющего соотношения упругого тела
![]()
Для резино-кордного
композита потенциал ![]() помимо
тензора дисторсии является еще и функцией координат. Мы предполагаем, что
деформации, возникающие в резине и в корде с разумной для практики точностью
можно считать малыми. Другими словами, в качестве потенциала
помимо
тензора дисторсии является еще и функцией координат. Мы предполагаем, что
деформации, возникающие в резине и в корде с разумной для практики точностью
можно считать малыми. Другими словами, в качестве потенциала![]() будем
использовать квадратичную функцию тензора деформаций Коши-Грина
будем
использовать квадратичную функцию тензора деформаций Коши-Грина ![]()
![]() (1.12)
(1.12)
Обычно деформации не превышают 10 процентов. Для таких значений деформаций представляется возможным использовать квадратичную функцию для упругой энергии деформации.
2. Пошаговый метод решения краевых задач неоднородной нелинейной теорииупругости.
Уравнения
и соотношения (1.8) - (1.11) представляют собой нелинейную систему уравнений
в частных производных относительно неизвестной вектор - функции ![]() (или вектора перемещения
(или вектора перемещения ![]() ).
Для численного решения краевой задачи (1.8) - (1.11) наиболее естественный
путь состоит в дискретизации по параметру нагружения t и в использовании
метода пошаговой линеаризации. Суть его состоит в следующем [23]. Если
решение для момента t известно, т. е. известен вектор
).
Для численного решения краевой задачи (1.8) - (1.11) наиболее естественный
путь состоит в дискретизации по параметру нагружения t и в использовании
метода пошаговой линеаризации. Суть его состоит в следующем [23]. Если
решение для момента t известно, т. е. известен вектор ![]() ,
то ищем приращение
,
то ищем приращение ![]() за
за ![]() с точностью до линейных членов относительно
с точностью до линейных членов относительно ![]()
![]()
Представляя ![]() ,
запишем уравнение равновесия в приращениях
,
запишем уравнение равновесия в приращениях
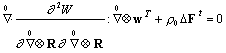
Таким образом, после дискретизации процесса деформирования на каждом шаге возникает задача типа краевой задачи неоднородной линейной теории упругости, для решения которой могут быть применены методы решения линейных задач. На каждом шаге компоненты тензора
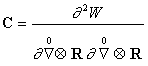
являются симметричными по парам индексов, поэтому задача в приращениях является самосопряженной, что существенно облегчает ее решение, особенно, при использовании итерационных методов. В целом, пошаговый метод описывается формулами
![]() (2.1)
(2.1)
![]()
![]() (2.2)
(2.2)
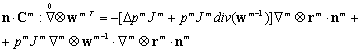 (2.3)
(2.3)
Можно улучшить аппроксимацию
за счет внутренних итераций. Если через ![]() обозначить s-ю итерацию к
обозначить s-ю итерацию к ![]() ,
причем
,
причем ![]() ,
то вместо формул (2.1) - (2.3) можно записать
,
то вместо формул (2.1) - (2.3) можно записать
![]() (2.4)
(2.4)
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
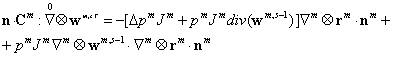 (2.7)
(2.7)
Такой подход целесообразно использовать только тогда, когда решение сильно изменяется относительно t .
3. Осреднение упругих свойств резино-кордного композита.
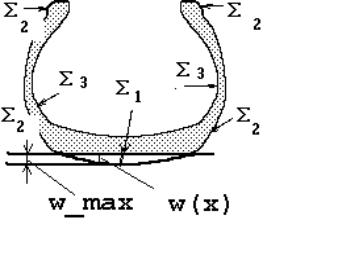
Хотя при использовании пошаговой линеаризации проблема свелась к линейной краевой задаче на каждом шаге, прямое численное решение последней вряд ли возможно вследствие сложной структуры шины или, другими словами, ее неоднородности. При этом имеется два масштаба неоднородности. Первый вызван наличием в структуре шины резино-корда и собственно резины. Второй масштаб связан уже только с резино-кордом, представляющим собой волокнистый композит, и определен толщиной слоев нитей или даже самих нитей при более точном рассмотрении структуры. Поэтому необходим промежуточный этап, заключающийся в осреднении упругих свойств резино-кордного композита. Точнее, следует применить методику осреднения [13] к задаче (2.4) - (2.7). Неоднородность упругих свойств первого масштаба приводит к необходимости на каждом шаге решать неоднородную краевую задачу (2.4) - (2.7), структура неоднородности которой показана на рис. 2. Однако резинокорд и брекер (тоже резино-корд) имеют внутреннюю структуру, учесть которую невозможно численным решением в "лоб", а можно только на основе метода осреднения, так как не хватит мощности никакого компьютера, чтобы осуществить дискретизацию всей конструкции на уровне масштаба волокон. В такой детальной дискретизации, впрочем, нет и необходимости, так как методика осреднения позволяет находить не только средние (или эффективные) упругие характеристики и поля перемещений и напряжений, но и приближенно их значения в отдельных компонентах структуры [13]. Как показали многочисленные исследования качество этого приближения весьма высоко.
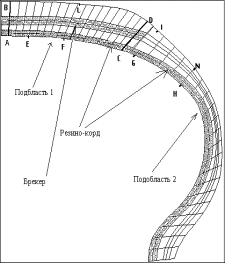
Рис. 2
В первом приближении решение задачи следует искать в виде
![]() (3.1)
(3.1)
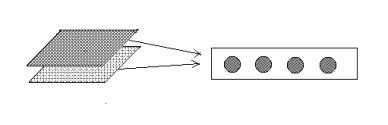
Рис 3.
Приближенность касается только
значений упругих компонентов, содержащих индекс 3. Это связано с тем, что
в этом направлении имеется только один слой волокон. Остальные компоненты
находятся точно.Однако, зависимость основных по величине напряжений от
этих констант слабая.Метод осреднения даже в первом приближении позволяет
не только определить НДС тела с осредненными или эффективными свойствами,
но и оценить флуктуации напряжений в компонентах структуры, что особенно
важно в вопросах прочности. Осредненное уравнение равновесия в приращениях
на шаге ![]() приобретает вид
приобретает вид
![]() (3.2)
(3.2)
и позволяет найти поле перемещений.
Ради упрощения записи индекс ![]() опущен.
опущен.