Глава
2. Численное моделирование осесимметричного напряженно-деформированного
состояния шин.
Описанная в первой
главе постановка задачи определения НДС шины реализована в виде программ
на Фортране. Отметим, что работа по отладке программ без поддержки ИНТАС
не могла бы быть выполнена. Пространственная дискретизация осуществлена
вариационно-разностным методом [12,17], который близок к МКЭ с изопараметрическими
элементами. Этот метод для областей с криволинейными границам был предложен
в [24] и подробно описан в [17]. Программная реализация осуществлена как
для случая осесимметричной деформации, так и для трехмерного случая. Из
вариационно-разностного метода на каждом шаге нагружения получается система
линейных уравнений, которая решается итерационным методом в трехмерном
случае и методом Холецкого в двумерном. Ниже приводятся результаты некоторых
расчетов, демонстрирующих возможности разработанной методики и программ.
1.
Осесимметричное напряженно-деформированное состояние шин
В данном пункте приведены
тестовые расчеты осесимметричной краевой задачи теории упругости о нагружении
шины nвнутренним давлением [18,19]. На рис. 2 приведена сетка для
области меридионального сечения, соответствующей геометрии шины. Сетка,
показанная на рис. 2, является довольно грубой. Однако на ней видно сгущение
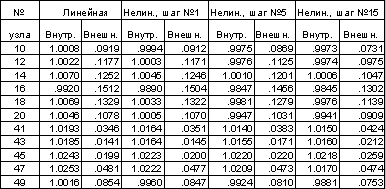
сетки в подобласти 1, где находятся брекер и резинокордная ткань. В таблице
1 приведены значения, полученные расчетным путем, нормальной к поверхности
шины компоненты напряжения

в задаче о нагружении шины внутренним давлением. Значения даны в узлах,
расположенных на внутренней и внешней поверхности и отнесены к действующему
давлению. Число узлов по толщине равно 12, а в другом направлении - 81.
Узлы с номерами 10-20 расположены между точками E
и F , а 41-49
- между G
и H. Исторически первый тест - это решение краевой задачи
теории упругости для однородного материала с упругими (безразмерными) постоянными:

,
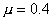
,
что соответствует
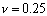
,
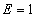
(все
величины, имеющие размерность напряжения, отнесены к внутреннему давлению).
Эти данные показывают точность вычислений, так как значения нормального
к поверхности напряжения должны равняться внешнему давлению на внутренней
поверхности ( =1 ) и нулю на внешней. Первая колонка таблицы содержит данные,
полученные при решении линейной задачи, последующие - нелинейной и соответствуют
первому, пятому и пятнадцатому шагам нагружения. Расчеты сделаны на сетке
15х81.
Таблица 1
На рис. 4a,
4b и 4c приведены компоненты напряжения, полученные при решении
однородной краевой задачи теории упругости в линейной и нелинейной постановках.
Эти напряжения взяты вдоль серединной линии меридионального сечения. Значения  ,
,  ,
,
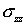
отнесены к значению внутреннего давления. Точке 0.89 соответствует
граница крепления шины на ободе колеса. На рисунках "лин" и "нелин" обозначают,
получено решение в геометрически линейной или нелинейной постановках. При
этом внутренне давление задано так чтобы деформация не превышала 10 процентов.
Различие в напряжениях наблюдается в областях, где деформации достигают
своего максимума. Различие результатов приводит к выводу о необходимости
использования геометрически нелинейной постановки задачи.
Второй тест - это
уже решение неоднородной задачи с анизотропными эффективными упругими свойствами,
характерными для каркаса и брекера. Расчеты сделаны на сетке17х65. Безразмерные
константы для резины были выбраны: 
,

,
что соответствует

,

.
Для кордных нитей каркаса

,

и для кордных нитей брекера
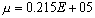
,
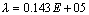
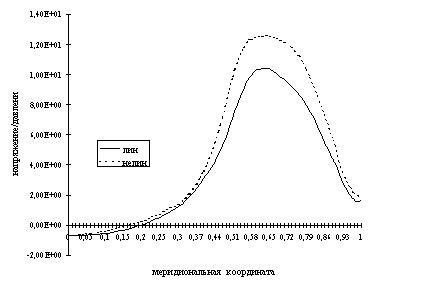
Рис. 4а - 

Рис. 4b - 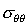
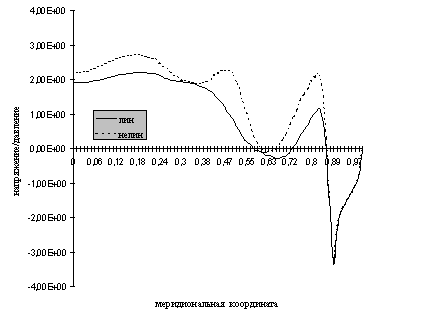
Рис. 4с - 
Безразмерное внутренне
давление - 0,05. Упругие размерные константы отнесены к удвоенному модулю
сдвига резины. Направляющие угли каркасных нитей составляют 0 градусов
относительно меридиана шины, а направляющие углы брекерных нитей  градусов.
Объемная концентрация для волокон каркаса взята 0.3, для волокон брекера
- 0.2. Осредненные упругие константы для каркаса и брекера получились равными:
градусов.
Объемная концентрация для волокон каркаса взята 0.3, для волокон брекера
- 0.2. Осредненные упругие константы для каркаса и брекера получились равными:
для каркаса: 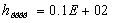 ,
,  ,
,  ,
,  ,
,
для брекера:
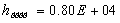
,

,

,

,
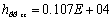
,
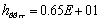
,

,

,

.
На рис. 5a,
5b и 5
c сравниваются напряжения

,

и

вдоль
линий AB, FL, CD, GI и HN (см. рис. 2), где точки 0 и 0,15 - границы области
каркаса, а 0,32 и 0,51 - брекера. Результаты показывают, что наибольшие
значения напряжения находятся в области брекера и каркаса.
Из рис. 5a наблюдается повышение
значение напряжение  в
области, где присутствует только каркас. Значение напряжение
в
области, где присутствует только каркас. Значение напряжение  максимально в области брекера (рис. 5b), а значение
максимально в области брекера (рис. 5b), а значение 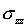 - в области каркаса (рис. 5c).
- в области каркаса (рис. 5c).
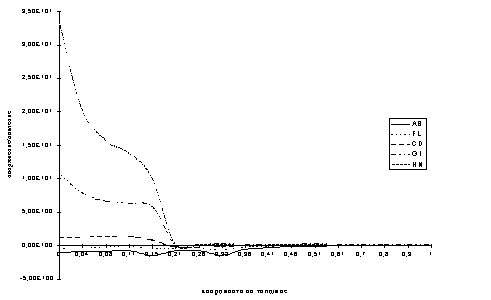
Рис. 5а - 

Рис. 5b - 

Рис. 5с - 
На рис. 6a
и
6b в направление AB (см. рис. 2) сравниваются значения  (i=1,2)
полученные при решении краевых задач об осадке шины о жесткую поверхность
для плоского деформированного (поверхность - плоскость) и осесимметричного
состояний (цилиндрическая жесткая поверхность). Эти задачи являются модельными
и призваны приближенно оценить НДС в меридиональном сечении, находящемся
в центре площадки контакта. На фигурах графику 1 соответствует решение
осесимметричной задачи с реальным радиусом шины, графику 2 - с пятикратным
увеличением радиуса шины, а графику 3 - задачи для плоского деформированного
состояния, где
(i=1,2)
полученные при решении краевых задач об осадке шины о жесткую поверхность
для плоского деформированного (поверхность - плоскость) и осесимметричного
состояний (цилиндрическая жесткая поверхность). Эти задачи являются модельными
и призваны приближенно оценить НДС в меридиональном сечении, находящемся
в центре площадки контакта. На фигурах графику 1 соответствует решение
осесимметричной задачи с реальным радиусом шины, графику 2 - с пятикратным
увеличением радиуса шины, а графику 3 - задачи для плоского деформированного
состояния, где  -
нормаль к внутренней поверхности. Видно, что для шины внутренним диаметром,
увеличенным в 5 раз, решения, полученные в рамках плоско деформированного
и осесимметричного состояний, близки. Поэтому такое решение близко и к
решению трехмерной задачи. Однако, для реального диаметра колеса из графиков
можно сделать вывод, что решение задачи об осадке, полученное в предположении
об осесимметричности НДС, не является достаточно точным. Для достоверного
решения задачи об осадке шины о твердую поверхность необходимо решать трехмерную
краевую задачу.
-
нормаль к внутренней поверхности. Видно, что для шины внутренним диаметром,
увеличенным в 5 раз, решения, полученные в рамках плоско деформированного
и осесимметричного состояний, близки. Поэтому такое решение близко и к
решению трехмерной задачи. Однако, для реального диаметра колеса из графиков
можно сделать вывод, что решение задачи об осадке, полученное в предположении
об осесимметричности НДС, не является достаточно точным. Для достоверного
решения задачи об осадке шины о твердую поверхность необходимо решать трехмерную
краевую задачу.

Рис. 6а -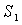 :
_____
3, _ _ _ 2, ------- 1
:
_____
3, _ _ _ 2, ------- 1

Рис. 6 -  :
____
3, _ _ _ 2, -------1
:
____
3, _ _ _ 2, -------1
Рассмотрим третий тест,
в котором сравниваются решения геометрически нелинейной задачи об упругой
однородной шине под действием внутреннего давления. Этот тест был призван
проверить трехмерную программу. В таблицах 2, 3 сравниваются напряжения,
полученные решением этой задачи как трехмерной и как осесимметричной. Напряжения
приведены вдоль линии AB на рис. 2. Значения напряжения отнесены
к значению давления. Расчеты сделаны на сетке9х9х65. Сравнение показывает
совпадение расчетов.
Tаблица
2
|
1 шаг инеаризации
|
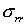
|

|
|
|
Осесим.
|
3D
|
Осесим.
|
3D
|
осесим.
|
3D
|
-9,43E-01
-9,39E-01
-8,25E-01
-7,62E-01
-6,32E-01
-8,34E-01
-2,97E-01
3,81E-02
-1,42E-01
|
-9,39E-01
-9,35E-01
-8,21E-01
-7,58E-01
-6,28E-01
-8,30E-01
-2,93E-01
4,14E-02
-1,38E-01
|
3,34E+00
3,40E+00
3,50E+00
3,56E+00
3,65E+00
3,63E+00
3,87E+00
4,05E+00
4,13E+00
|
3,35E+00
3,41E+00
3,51E+00
3,57E+00
3,66E+00
3,64E+00
3,87E+00
4,06E+00
4,14E+00
|
4,91E-01
8,95E-01
1,31E+00
1,66E+00
2,03E+00
2,33E+00
2,94E+00
3,70E+00
4,57E+00
|
4,93E-01
8,97E-01
1,32E+00
1,66E+00
2,03E+00
2,33E+00
2,94E+00
3,70E+00
4,57E+00
|
Таблица
3.
|
5 шаг линеаризации
|
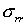
|
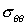
|

|
|
Осесим.
|
3D
|
Осесим.
|
3D
|
осесим.
|
3D
|
-9,18E-01
-9,12E-01
-7,94E-01
-7,28E-01
-5,94E-01
-7,87E-01
-2,46E-01
9,01E-02
-7,26E-02
|
-9,14E-01
-9,08E-01
-7,90E-01
-7,24E-01
-5,90E-01
-7,84E-01
-2,42E-01
9,32E-02
-6,94E-02
|
3,38E+00
3,44E+00
3,54E+00
3,60E+00
3,68E+00
3,65E+00
3,89E+00
4,08E+00
4,16E+00
|
3,39E+00
3,45E+00
3,54E+00
3,60E+00
3,68E+00
3,66E+00
3,90E+00
4,08E+00
4,16E+00
|
8,68E-01
1,26E+00
1,67E+00
2,00E+00
2,36E+00
2,64E+00
3,25E+00
4,01E+00
4,92E+00
|
8,71E-01
1,26E+00
1,67E+00
2,01E+00
2,36E+00
2,65E+00
3,26E+00
4,01E+00
4,92E+00
|

![]() ,
, ![]() ,
,

![]()

![]()

![]()
![]() градусов.
Объемная концентрация для волокон каркаса взята 0.3, для волокон брекера
- 0.2. Осредненные упругие константы для каркаса и брекера получились равными:
градусов.
Объемная концентрация для волокон каркаса взята 0.3, для волокон брекера
- 0.2. Осредненные упругие константы для каркаса и брекера получились равными:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,


![]()


![]() (i=1,2)
полученные при решении краевых задач об осадке шины о жесткую поверхность
для плоского деформированного (поверхность - плоскость) и осесимметричного
состояний (цилиндрическая жесткая поверхность). Эти задачи являются модельными
и призваны приближенно оценить НДС в меридиональном сечении, находящемся
в центре площадки контакта. На фигурах графику 1 соответствует решение
осесимметричной задачи с реальным радиусом шины, графику 2 - с пятикратным
увеличением радиуса шины, а графику 3 - задачи для плоского деформированного
состояния, где
(i=1,2)
полученные при решении краевых задач об осадке шины о жесткую поверхность
для плоского деформированного (поверхность - плоскость) и осесимметричного
состояний (цилиндрическая жесткая поверхность). Эти задачи являются модельными
и призваны приближенно оценить НДС в меридиональном сечении, находящемся
в центре площадки контакта. На фигурах графику 1 соответствует решение
осесимметричной задачи с реальным радиусом шины, графику 2 - с пятикратным
увеличением радиуса шины, а графику 3 - задачи для плоского деформированного
состояния, где ![]() -
нормаль к внутренней поверхности. Видно, что для шины внутренним диаметром,
увеличенным в 5 раз, решения, полученные в рамках плоско деформированного
и осесимметричного состояний, близки. Поэтому такое решение близко и к
решению трехмерной задачи. Однако, для реального диаметра колеса из графиков
можно сделать вывод, что решение задачи об осадке, полученное в предположении
об осесимметричности НДС, не является достаточно точным. Для достоверного
решения задачи об осадке шины о твердую поверхность необходимо решать трехмерную
краевую задачу.
-
нормаль к внутренней поверхности. Видно, что для шины внутренним диаметром,
увеличенным в 5 раз, решения, полученные в рамках плоско деформированного
и осесимметричного состояний, близки. Поэтому такое решение близко и к
решению трехмерной задачи. Однако, для реального диаметра колеса из графиков
можно сделать вывод, что решение задачи об осадке, полученное в предположении
об осесимметричности НДС, не является достаточно точным. Для достоверного
решения задачи об осадке шины о твердую поверхность необходимо решать трехмерную
краевую задачу.


![]() :
____
3, _ _ _ 2, -------1
:
____
3, _ _ _ 2, -------1