где ![]() -
сеточная функция перемещений,
-
сеточная функция перемещений, ![]() -
правая часть, включающая в себя объемные, а на границе и поверхностные
силы,
-
правая часть, включающая в себя объемные, а на границе и поверхностные
силы, ![]() - разностный оператор, являющейся симметричным и отрицательно определенным:
- разностный оператор, являющейся симметричным и отрицательно определенным: ![]() .
Для задач связанной с шиной оператор
.
Для задач связанной с шиной оператор ![]() является достаточно плохо обусловленным вследствие сложной геометрией области
и сильной неоднородности материала. Для решения задачи используем двухслойный
и трехслойный итерационные процессы [17, 20, 21], записываемые в виде
является достаточно плохо обусловленным вследствие сложной геометрией области
и сильной неоднородности материала. Для решения задачи используем двухслойный
и трехслойный итерационные процессы [17, 20, 21], записываемые в виде
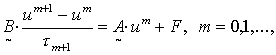 (1.2)
(1.2)
или соответственно
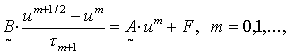 (1.3)
(1.3)
![]()
где ![]() -е
приближение к решению
-е
приближение к решению ![]() ,
, ![]() –
некоторый самосопряженный и положительно определенный оператор,
–
некоторый самосопряженный и положительно определенный оператор, ![]() -
итерационные параметры. Терминология, используемая при описании рассматриваемых
уравнений, может быть двоякой. Можно говорить о сеточных функциях и о разностных
операторах и уравнениях [17, 20], а можно говорить о векторах, матрицах
и алгебраических уравнениях (линейных и нелинейных) [6]. Оба способа описания
эквивалентны. Для оценки скорости сходимости процесса (1.2) будем использовать
норму
-
итерационные параметры. Терминология, используемая при описании рассматриваемых
уравнений, может быть двоякой. Можно говорить о сеточных функциях и о разностных
операторах и уравнениях [17, 20], а можно говорить о векторах, матрицах
и алгебраических уравнениях (линейных и нелинейных) [6]. Оба способа описания
эквивалентны. Для оценки скорости сходимости процесса (1.2) будем использовать
норму![]() ,
порождаемую скалярным произведением
,
порождаемую скалярным произведением
![]()
причем
разностный оператор ![]() выберем в виде
выберем в виде ![]() [ 17, 20]. Такой выбор позволяет контролировать сходимость итераций, так
как величина
[ 17, 20]. Такой выбор позволяет контролировать сходимость итераций, так
как величина ![]() вычислима.
вычислима.
При
конструировании итерационных процессов, которые должны применяться при
решении практических задач, два вопроса являются ключевыми. Во-первых,
следует выбрать оператор ![]() ,
во-вторых, нужно уметь оптимально выбирать параметры
,
во-вторых, нужно уметь оптимально выбирать параметры ![]() .
Оператор
.
Оператор ![]() желательно выбрать так, чтобы он был легко обратим и между ним и оператором
-
желательно выбрать так, чтобы он был легко обратим и между ним и оператором
- ![]() существовала спектральная (или энергетическая ) эквивалентность [3, 4,
17, 20]
существовала спектральная (или энергетическая ) эквивалентность [3, 4,
17, 20]
![]() (1.4)
(1.4)
с
константами ![]() ,
не зависящими от шагов сетки. Неравенства (1.4) подробнее записываются
в виде
,
не зависящими от шагов сетки. Неравенства (1.4) подробнее записываются
в виде
![]()
В
качестве оператора ![]() мы выбираем или разностный оператор Лапласа в “канонической” области
мы выбираем или разностный оператор Лапласа в “канонической” области ![]() или
оператор, соответствующий неполному разложению Холецкого [31] (в последнем
случае эквивалентность осуществляется приближенно).В первом случае область
или
оператор, соответствующий неполному разложению Холецкого [31] (в последнем
случае эквивалентность осуществляется приближенно).В первом случае область ![]() является параллелепипедом, а для обращения оператора
является параллелепипедом, а для обращения оператора ![]() мы используем быстрый метод преобразования Фурье.
мы используем быстрый метод преобразования Фурье.
Теперь
о выборе итерационных параметров, от которых при выбранном переобуславливателе
собственно и зависит эффективность метода. Аналитически не представляется
возможным найти хорошие приближения для ![]() ,
которые необходимы для использования чебышевского процесса, когда параметры
выбираются по формуле
,
которые необходимы для использования чебышевского процесса, когда параметры
выбираются по формуле
![]() (1.5)
(1.5)
в случае двухслойного процесса, и по формуле
![]() (1.6)
(1.6)
в
случае трехслойного метода, где ![]() -
длина чебышевского цикла,
-
длина чебышевского цикла, ![]() Скорость сходимости чебышевских процессов (1.2), (1.3), является наибольшей
согласно теоретической оценке. Заметим, правда, что метод сопряженных градиентов
теоретически имеет скорость сходимости не хуже. Эта оценка определяется
выражениями
Скорость сходимости чебышевских процессов (1.2), (1.3), является наибольшей
согласно теоретической оценке. Заметим, правда, что метод сопряженных градиентов
теоретически имеет скорость сходимости не хуже. Эта оценка определяется
выражениями
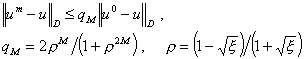 (1.7)
(1.7)
Конечно,
формулы (1.7) справедливы лишь в случае отсутствия ошибок округления и
когда константы ![]() заданы точно. В реальных вычислениях следует предварительно приближенно
определить константы
заданы точно. В реальных вычислениях следует предварительно приближенно
определить константы ![]() ,
а итерации приходится проводить при наличии накопления ошибок округления
и неточности в задании констант
,
а итерации приходится проводить при наличии накопления ошибок округления
и неточности в задании констант ![]() .
Поэтому для практической реализации итераций нужно решить еще некоторые
вопросы, от решения которых напрямую зависит практическая ценность метода.
.
Поэтому для практической реализации итераций нужно решить еще некоторые
вопросы, от решения которых напрямую зависит практическая ценность метода.
Первый
вариант решения состоит в приближенном определении констант эквивалентности
и последующем их уточнении. Для определения ![]() используем
градиентный метод, имеющий вид (1.2), но параметры
используем
градиентный метод, имеющий вид (1.2), но параметры ![]() в
нем определяются апостериорно по предыдущему приближению в процессе итераций
[17, 20]
в
нем определяются апостериорно по предыдущему приближению в процессе итераций
[17, 20]
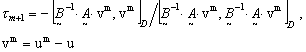 (1.8)
(1.8)
Скорость сходимости этого метода, определяемая величиной
![]()
где ![]() -
невязка m - го приближения, как показывает теория и численные эксперименты,
быстро падает, т.е.
-
невязка m - го приближения, как показывает теория и численные эксперименты,
быстро падает, т.е. ![]() выходит на константу, близкую к единице. Однако после выхода величины
выходит на константу, близкую к единице. Однако после выхода величины ![]() на
асимптоту, как показано в [20], приближенные значения констант
на
асимптоту, как показано в [20], приближенные значения констант ![]() находятся как корни квадратного уравнения
находятся как корни квадратного уравнения